Thread: iPhone 15 / Apple Watch 9 Event
- Thread starter exoticspice1
- Start date
- Joined
- Sep 26, 2021
- Posts
- 6,150
- Main Camera
- Sony
The recent rule is 5am pacific.
- Joined
- Aug 10, 2020
- Posts
- 12,841
- Solutions
- 18
- Main Camera
- Sony
I'll let my avatar speak to my readiness at that exact time.
Andropov
Site Champ
- Joined
- Nov 8, 2021
- Posts
- 712
Finding rigorous explanations for this topic is extremely frustrating, because many formulas implicitly assume one of the variables as constant (sensor size, field of view...).
You're right that halving the subtended angle of what you're viewing reduces the amount of photons that reach us to 1/4. But who says that increasing the focal length has to reduce our viewing angle? That's only true if the sensor size is constant! The formula for the field of view (fov) of a lens is:
So, if we increase the sensor width proportionally to the focal length, we can keep the same field of view with a longer focal length. For example, if we double the focal length but keep the same fov, the amount of light captured isn't reduced to 1/4. What changes, however, is that our image circle must be bigger (4 times the original area) to capture the same fov. The aperture size hasn't changed, and neither has our viewing angle, yet this lens has a different f-number. The light-gathering capabilities of the system remain the same (same fov, same aperture), but the amount of light per unit area has been reduced to 1/4 (we're projecting the same amount of light over an area 4 times as big). That's what remains constant for the same f number, not the total amount of light gathered.
Another example: if you switch a given lens (let's say, a 50mm f/1.4) from a full frame to an APS-C camera, you undoubtedly still have a f/1.4 lens, but you'll only be able to capture ~61.8% as much light total as before, because the sensor is smaller (and your images will have a narrower fov too, but that's not relevant to how much light we capture). What has remained constant? The amount of light in the sensor *per unit area*, which is obvious in hindsight because you're essentially just "cropping" a smaller part of the image circle the lens has.
That said, it doesn't help discussions one bit that focal lengths of smartphones are often given as the 35 mm equivalent focal length. That means that the magnitude we're dealing with is no longer a measure of the focal length, but rather the focal length a camera with a 35mm sensor would need to have to have the same fov. So it becomes essentially a different unit to measure fov, not focal lenght.
Andropov
Site Champ
- Joined
- Nov 8, 2021
- Posts
- 712
I think what's different here, compared to competitors, is that apple is using a prism instead of a set of mirrors, but I don't think periscope designs are inherently limited as to how many reflections are allowed inside.
Btw, I'm finding it a bit funny reading people on the internet saying that tetraprism is somehow a made-up marketing name by Apple. Pentaprism / pentamirror is a pretty standard term when discussing DSLR viewfinders, and it's not outrageous that Apple wants to emphasize that they are using a prism rather than a set of mirrors, as it's a better setup (less light loss, less susceptible to misalignment...).
I'm afraid I'm not following. Let's suppose you point your camera at a building with equally-spaced dimly-lit windows of equal size, and want to take a picture of just one of those windows at night, and want as much light-gatherng as possible (hmm, just realized that sounds a bit creepy...). It seems to me that the brightness of the image you capture is going to be determined by the angle that one window subtends, irrespective of the the fov of your camera, and will thus be independent of your sensor size.
What you're describing (having a larger fov on a larger sensor) just means you are, say, shining the light from ≈1.6 windows across your sensor (ignoring the spacing between the windows). Yes, there's more light coming in, but that's just because you're capturing extraneous light (from the 2nd window) that's not actually part of your desired picture. Further, this approach reduces the resolution, because instead of using the whole sensor to capture your window, you're using only part of it.
I.e., what you're describing with the larger sensor is taking a wider-angle picture (which of course has more total light), and then cropping the image down to just to the one window you want. [I believe this is what "digital zoom" does.] As far as I can tell, the total light you get from that one window is not increased by this, i.e., it is not increased by a larger sensor.
Amusingly, there's a thread about this on DPReview, in which arguments are presented for both sides, that goes on for eight pages (!) with no apparent resolution (no pun intended).
Last edited:
Nycturne
Elite Member
- Joined
- Nov 12, 2021
- Posts
- 1,374
Not quite. But on the right track. Consider the scenario of two cameras next to each other. They both capture light from the window, I have captured more light if I combine the two cameras than either camera did individually. So there is more light available if I have more area to capture light with. But a sensor by itself doesn't capture light. It's the whole system that captures light.
Low light performance is a tricky beast. For extended objects, it's aperture that determines how much light is captured from the object, and focal length determines the extent of the object at the focal plane. Together we get f-ratio. So consider this other scenario: Same sensor, same focal length lens. Only one is configured with a wider aperture. So you go from f/4 to f/2.8. Ultimately, the field of view is identical, but we can demonstrate that the f/2.8 captures more light per unit of time. But you can also demonstrate that two cameras with the same f-ratio and fov (note, not focal length) will have similar results for the same exposure time. Because f-ratio itself simplifies the system down to the important bits when discussing exposure time (which is a result of light capture).
And then you can get into the regime of astrophotography where certain things get even more important as read noise is suddenly no longer a negligible impact on SNR. Fun.
I disagree with "not quite". If you carefully re-read my original post on this, you'll see you're saying the same thing I did. What you're describing by having two identical cameras is equivalent to increasing the value of D (the entrance diameter, aka aperture) by a factor of sqrt(2). I think what you misunderstood is that, in the paragraph you quoted, I was considering the amount of light you capture from the specific scene you want to photograph, which in this case was one window. What determines the light emitted by that window isn't your fov, since increasing the fov doesn't increase the light from that specific window, it just means you capture additional extraneous light.
Suppose you're photographing a scene that is part of a uniformly-lit surface, from a fixed distance. Simply put, the number of photons the scene emits is proportional to angle the scene subtends (larger angle ⇒ more surface area ⇒ more photons), and the fraction of those emitted photons your camera captures is proportional to the lens's entrance diameter, D (aka aperture). [The latter proportionality should be photons ~ D^2, as mentioned earlier, barring any intervening effects.]
Last edited:
Does anyone know the fastest way to get to my "bag" when zero hour arrives on Friday morning? The email I got from Apple contained a calendar appointment with a link that goes to the "come back on 9.15" page. The appointment also says I can use the App Store mobile app, but my bag there is empty. I wonder if that'll change at the appointed time?
Nycturne
Elite Member
- Joined
- Nov 12, 2021
- Posts
- 1,374
Agreed on the side of emission and that FOV is not a great way to describe it. But this phrase muddies things a bit: "It seems to me that the brightness of the image you capture is going to be determined by the angle that one window subtends, irrespective of the the fov of your camera, and will thus be independent of your sensor size." And I was getting hung up on that, but it's why I say it was not quite.
It really helps to avoid thinking of things in terms of emission, and ignore image circle size as well for a moment. An extended object will emit what it emits, and an image circle is about as relevant as sensor size. What we're interested in is optimizing photon capture. And your original post does cover that well, because f-ratio is the factor that matters when comparing two systems. So getting back to your original post:
"So at least based on this, f is a measure of the light-gathering capability of the optical device, and it's independent of sensor size."
Absolutely correct. Smaller sensors "crop" when compared to larger sensors, but don't do anything else. Effective focal length numbers tend to mess with things, but focal ratio should still be from the real focal length, not effective. So Apple's focal ratio numbers should be comparable to other systems.
"Thus if you have a lens of a given f-value, you should have a constant amount of light falling onto the image circle, not a constant amount of light per unit area. But maybe I'm confused!"
This is backwards. The same f-ratio in two different lenses at the same target produce the same amount of light per unit area. If I use a full-frame lens on an APS-C camera at the same f-ratio, the two images will be equally bright. If aperture tells me how much light I can capture, focal length tells me how spread out that light is. So long as the ratio is the same, the light per unit area is the same. This is why I used the examples I did where aperture changes. I can keep the "extent of the object" constant, but still affect brightness of an image. With a crop sensor, I can use a shorter focal length to get the same FOV with the smaller image circle, and a smaller aperture to produce the same f-ratio. So that accounts for not needing to spread as much light across a larger image circle right there and helps confirm that f-ratio tells us something about the light per unit area.
But again, this also assumes we aren't in a regime where sensor noise doesn't become important, which it does in low-light photography, especially when sensors can be pretty noisy, which is more common in these smaller sensors that aren't well isolated from everything else and have to deal with the heat coming off your SoC/etc. Once you get into that regime, then things get more complex, as the above assumes you have enough signal to remain above the noise (other than shot noise).
Jimmyjames
Elite Member
- Joined
- Jul 13, 2022
- Posts
- 1,085
Seems like the usual sources have already labeled the A17 as the A16 redux and a “stopgap chip”. Sigh. We don’t even have any tests for these and the negative framing begins.
- Joined
- Sep 26, 2021
- Posts
- 6,150
- Main Camera
- Sony
Apple told us it’s more than that (e.g. wider dispatch and execute.). I suppose I’m supposed to believe this name kremlinology and ignore what apple actually tells us?
Jimmyjames
Elite Member
- Joined
- Jul 13, 2022
- Posts
- 1,085
Lol indeed. The frenzy people are working themselves into.
OK, good. Now we're getting to the essence of it. I suspected this was why your view is different from mine, and this confirms it. And, needless to say, I don't believe it's me that has it backwards
. But we shall see....I believe this first diagram illustrates the picture you have of how modern digital cameras work. We agree (I hope) that, for a given level of outside illumination, the total photon flow onto the respective light circles is determined only by the f-value, which accounts for both the lens aperture and the angle the scene subtends. [I'm ignoring light loss due to the camera lens material, etc.]
If you use a lens designed for a large-sensor camera on one with a small sensor, the following is indeed what happens, corresponding to your description: You have the same photon flow/unit area, so the smaller sensor captures less light. But that's obvously not how you want to design a camera, since you're throwing away all that precious light.
Wikipedia has a good description of this lens mismatch: "Lenses produced for 35 mm film cameras may mount well on the digital bodies [of small-sensor cameras], but the larger image circle of the 35 mm system lens allows unwanted light into the camera body, and the smaller size of the image sensor compared to 35 mm film format results in cropping of the image. [Emphasis mine.] This latter effect is known as field-of-view crop."
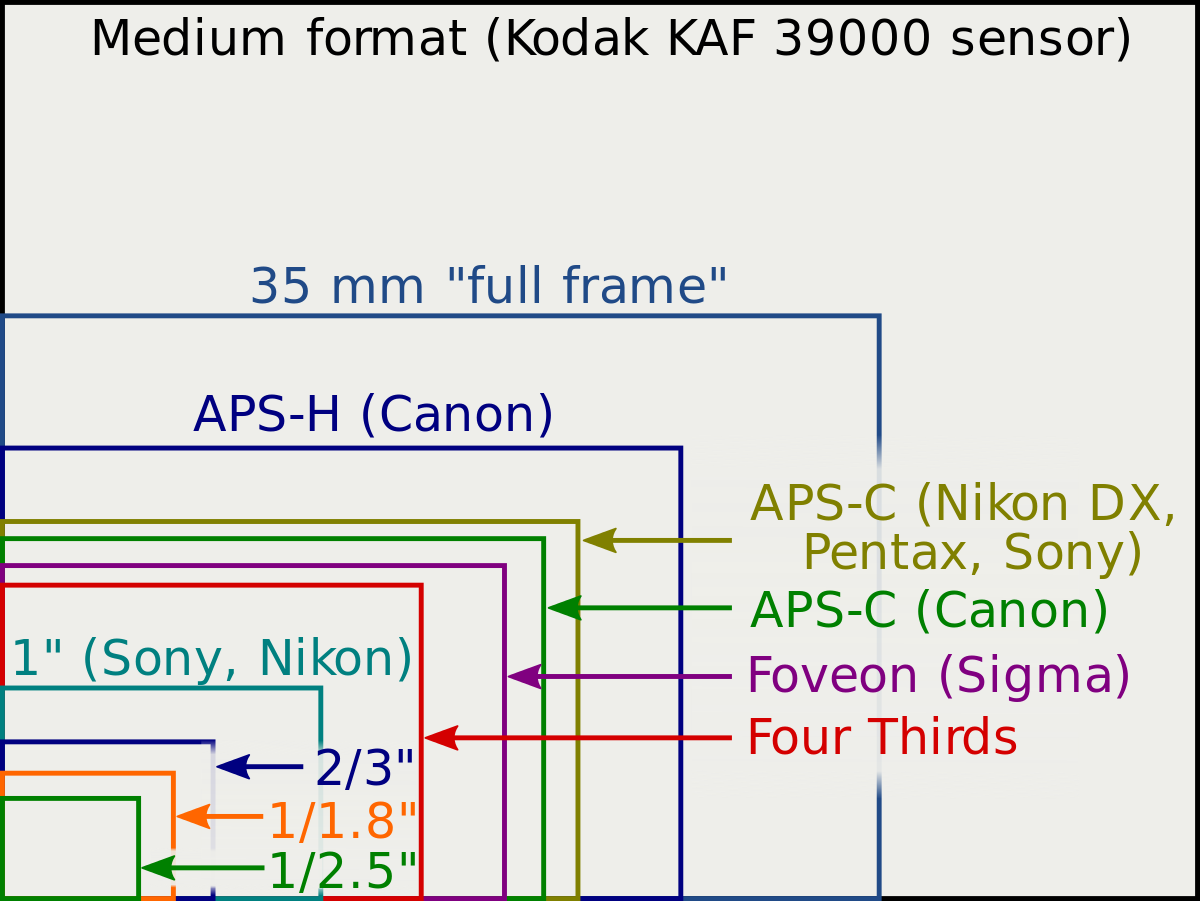
Image sensor format - Wikipedia
Instead, in a properly-designed digital camera, the lens/sensor system should be configured to give a light circle that corresponds to the sensor size, as illustrated by the diagram below. Thus smaller sensors don't crop any more than larger ones do (assuming constant sensor aspect ratio) (ignoring specific design decisions that might alter this slightly).
If these two cameras have the same f-value, it's again the case that the total photon flow onto their respective light circles is the same. But now the light circle for the small-sensor camera is focused on a smaller area, to properly correspond to its sensor size, which means the total light falling onto both sensors is (about*) the same (and the photon flow/unit area is higher for the small sensor, since the same amount of light is focused onto a smaller area).
Designing the camera-lens system so the light circle size matches the sensor size enables cameras with small sensors to perform far better in low-light situations.
*I suspect that, for both large and small-sensor cameras, it is optically tricky to maintain a relatively constant light circle size, and thus a constant crop factor, as you change focal length, but that's part of the challenge of modern camera optics. [And, as I mentioned earlier, you might occasionally have other requirements that necessitating deliberately designing different crop factors, due to variations in vignetting, optical quality at the lens edge, the desire to introduce lens shift, etc.]
Last edited:
- Joined
- Aug 11, 2020
- Posts
- 6,167
- Solutions
- 2
So much better than in the past when it was 10 pm Pacific!
- Joined
- Sep 26, 2021
- Posts
- 6,150
- Main Camera
- Sony
There was a time when it was midnight, and it didn’t actually work sometimes until later.
exoticspice1
Site Champ
- Joined
- Jul 19, 2022
- Posts
- 365
Looks like since A14 Apples been resting. Less than 2% IPC increase and most of speed increases are from clocks.
If the A17 CPU was clocked at A14 levels the score would be the around same, indicating little IPC improvements within 3-4 years.
The GPU team is doing more work than the CPU lately.
- Joined
- Sep 26, 2021
- Posts
- 6,150
- Main Camera
- Sony
That’s a lot of conclusions to draw from fake scores
exoticspice1
Site Champ
- Joined
- Jul 19, 2022
- Posts
- 365
It's not fake. Here. https://browser.geekbench.com/search?q=iphone16,1
Jimmyjames
Elite Member
- Joined
- Jul 13, 2022
- Posts
- 1,085
Wow. If these are confirmed it looks bad.
EDIT: Hmmmm Geekbench scores are not reliable. Here’s the 15 Pro Max scoring…lower?
Geekbench Search - Geekbench
browser.geekbench.com
Here’s the 15 Pro Max scoring… between the 13 Pro and 14 Pro?? Oh and 16gb of ram…and an old OS.
Geekbench Search - Geekbench
browser.geekbench.com
We need to wait. Not saying those original scores are wrong, just that we need confirmation.
EDIT2: I truly don’t understand why a 3nm chip would need to increase frequency to gain an increase in performance vs a 5nm chip. Again I could be talking nonsense, but I thought the whole thing was 10~15% increase at the same iso power.
EDIT3: lol under the cpu name it says ARM. Instead of “Apple A17 Pro” or something similar. Since when have Apple named their cpu ARM. Lol. Fake.
Last edited:
